Section 4: Rational Exponents
It is important the you watch this video first.
Definition of a Rational Exponent.
am/n = (n√a)m
In general, if 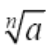 is a real number, then
is a real number, then
a1/n = 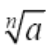
The denominator of a fractional exponent is equal to the index of the radical.
So 81/3 is the exponential form of the cube root of 8, and 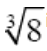 is its radical form.
is its radical form.
Next, we ask: what sense can we make of a symbol like a2/3? According to the rules of exponents:
a2/3 = (a1/3)2 or a2/3 = (a2)1/3
Example:
Use can use either of these rules to simplify the expression 82/3 as shown below.
Solution:
82/3 = (81/3)2 = 22 = 4
or
82/3 = (82)1/3 = 641/3 = 4
Notice that we get the same answer either way. However, to evaluate a fractional power, it is more efficient to take the root first.

The denominator of a fractional exponent indicates the root.
Specifically, 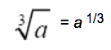 or in general:
or in general: 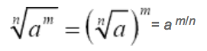
Notice: The index of the radical becomes the denominator of the rational power, and the exponent of the radicand (expression inside the radical) becomes the numerator.
Test Your Knowledge by opening up the Test Yourself Activity.
Contact Us
For more information about the TSI Assessment and how to register, visit https://www.hccs.edu/resources-for/current-students/testing-services/ or email hcc.testing@hccs.edu

