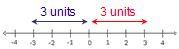Section 2: Solving Absolute Value Equations
It is important that you watch the video first.
Solving Absolute Value Equations of the Type | x | = k.
Absolute value equations are useful in determining distance and error measurements.
| The examples that we will consider are: | ||
|---|---|---|
| | x | = 3 | | x – 6 | = 4 | | 2x – 3 | = 9 |
| | x + 7 | = –2 | | x + 8 | = | 3x – 4 | | |
Example 1 : Solve for x: | x | = 3
Solution.
This equation is asking us to find all numbers, x, that are 3 units from zero on the number line.
We must consider numbers both to the right and to the left of zero on the number line.
Notice that both 3 and -3 are three units from zero.
The solution is: x = 3 or x = −3.
Example 1 suggests a rule that we can use when solving absolute value equations.
If c is a positive number, then | x | = c is equivalent to x = c or x = –c.
Example 2 : Solve for x: | x – 6 | = 4
Solution.
Step 1. Break the equation up into two equivalent equations using the rule: If |x| = c then x = c or x = -c.
| x – 6 | = 4 is equivalent to x – 6 = 4 or x – 6 = – 4
Step 2. Solve each equation.
| Solve each equation | |
|---|---|
| x – 6 + 6 = 4 + 6 x = 10 |
x – 6 + 6 = – 4 + 6 x = 2 |
Step 3. Check the solutions.
| 10 – 6 | = | 4 | = 4
| 2 – 6 | = | –4 | = 4
The solutions are x = 10 and x = 2.
Example 3 : Solve for x: | 2x – 3 | = 9
Solution.
Step 1. Break the equation up into two equivalent equations using the rule: If |x| = c then x = c or x = -c.
| 2x – 3 | = 9 is equivalent to 2x – 3 = 9 or 2x – 3 = -9
Step 2. Solve each equation.
2x – 3 = 9 or 2x – 3 = -9
2x – 3 + 3 = 9 + 3 or 2x – 3 + 3 = -9 + 3
2x = 12 or 2x = -6
2x ÷ 2 = 12 ÷ 2 or 2x ÷ 2 = -6 ÷ 2
x = 6 or x = -3
Step 3. Check the solutions.
x = 6: | 2(6) – 3 | = | 12 – 3 | = | 9 | = 9
x = -3: | 2(-3) – 3 | = | -6 – 3 | = | -9 | = 9
The solutions are x = 6 and x = -3
Example 4 : Solve for x: | x + 7 | = –2
Solution.
The absolute value of a number is never negative. This equation has no solution.
Solving Absolute Value Equations of the Type | x | = | y |.
If the absolute values of two expressions are equal, then either the two expressions are equal, or they are opposites.
If x and y represent algebraic expressions, | x | = | y | is equivalent to x = y or x = –y.
Example 5 : Solve for x: | x + 8 | = | 3x – 4 |
Solution.
Step 1. Break the equation up into two equivalent equations.
| x + 8 | = | 3x – 4 | is equivalent to x + 8 = 3x – 4 or x + 8 = –(3x – 4)
Step 2. Solve each equation.
x + 8 = 3x – 4 or x + 8 = –(3x – 4)
x + 8 = 3x – 4 or x + 8 = –3x + 4
x + 8 – x = 3x – 4 – x or x + 8 + 3x = -3x + 4 + 3x
8 = 2x – 4 or 4x + 8 = 4
8 + 4 = 2x – 4 + 4 or 4x + 8 – 8 = 4 – 8
12 = 2x or 4x = – 4
12 ÷ 2 = 2x ÷ 2 or 4x÷ 4 = – 4 ÷ 4
6 = x or x = – 1
Step 3. Check the solutions.
|
x = 6: | 6 + 8 | = | 3(6) – 4 | | 14 | = | 18 – 4 | 14 = 14 |
x = –1: | –1 + 8 | = | 3(–1) – 4 | | 7 | = | –3 – 4 | | 7 | = | –7 | 7 = –7 |
|---|---|
|
The solutions are x = 6 and x = – 1. | |
Test Your Knowledge by opening up the Test Yourself Activity.
Contact Us
For more information about the TSI Assessment and how to register, visit https://www.hccs.edu/resources-for/current-students/testing-services/ or email hcc.testing@hccs.edu