Section 4: Dividing Polynomials

Dividing a Polynomial by a Monomial

In a previous section, you learned how to divide a monomial by a monomial by applying rules of exponents.

For example, .

Division can be checked by multiplying: 2x ^. 5x² = 10x³.

In division, the number that is being divided is called the dividend, the number that is dividing into a number is called the divisor, and the answer to a division problem is called the quotient.

To divide a polynomial by a monomial, we divide each term of the polynomial by the divisor. (12x⁴ – 3x² + 6)(-3x) can be divided as follows:

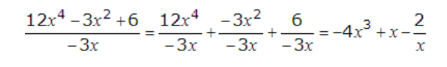
In this case the quotient is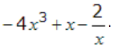 

Example 1. Find each quotient.

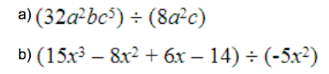
Solution.

a)  Apply the rules of exponents and subtract the exponents

b)  Divide each term of (15x3 – 8x2 + 6x – 14) by (-5x2):

Dividing a Polynomial by a Binomial

To divide a polynomial by a binomial, we use a procedure similar to long division.

We know that (2x – 7)(x + 4) = 2x² + x– 28. This implies that (2x² + x – 28) ÷ (x + 4) = 2x – 7. We can use long division, just like the example shown above with whole numbers, to illustrate the division process.

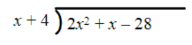
Find the first term of the quotient by dividing the first term of the dividend by the first term of the divisor:

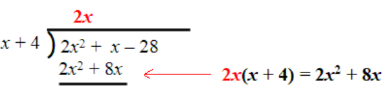
We need to subtract terms under the dividend and then carry down the last term and repeat the process.

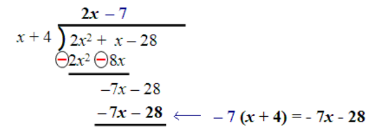
Here we can subtract and see that we have zero left as the remainder. The quotient is 2x – 7.

It is important to have the division set up properly before beginning. Each term in the divisor and the dividend must be listed in descending order. It is also helpful to fill in any missing terms using a coefficient of zero. The example below illustrates this.

 Example 2. Divide the polynomial: (8x³ – 27) ÷ (x – 3)

Solution.

Set up the division problem, filling in the missing terms using zeros as the coefficients.

Find the first term of the quotient by dividing the first term of the dividend by the first term of the divisor:

We need to subtract terms under the dividend and then carry down the next term and repeat the process. 

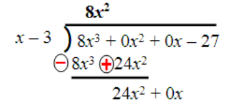
Find the second term of the quotient by dividing 24x² by the first term of the divisor: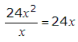 

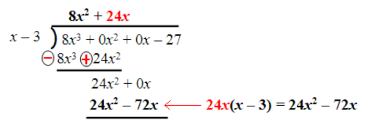
Subtract terms under the dividend and then carry down the last term. Then repeat the process.\

carry down last term

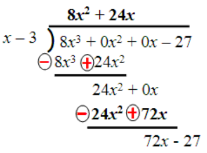
Find the third term of the quotient by dividing 72x by the first term of the divisor: 

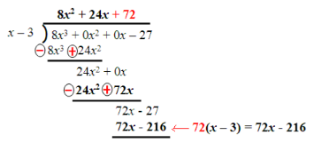
Here we can subtract and see that we have –243 left as the remainder. The quotient is 8x² + 24x + 72.

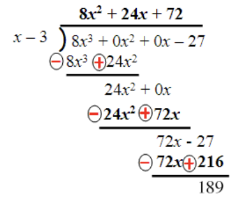
We can also express the results of this division in the form

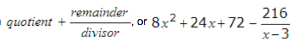
 Test Your Knowledge by opening up the Test Yourself Activity.