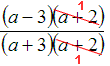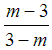Section 1: Simplifiying Rational Expressions
It is important that you watch the video first.
Write Rational Expressions in Lowest Terms
Just like arithmetic fractions, rational expressions should be written in lowest terms. The following property explains why we are able to simplify rational expressions.
Fundamental Property of Rational Numbers
If is a rational number and if c is any nonzero real number, then
That is, the numerator and denominator of a rational number may either be multiplied or divided by the same nonzero number without changing the value of the rational number.
The following steps will help you to write rational expressions in lowest terms:
Write a Rational Expression in Lowest Terms
Step 1- Factor both the numerator and denominator to find their greatest common factor (GCF).
Step 2- Apply the fundamental property of rational numbers.
Example 1:
Write the rational expression in lowest terms:
Solution:
The GCF of both the numerator and denominator is 8. Therefore, we can use the fundamental property of rational numbers to divide both the numerator and denominator by 8, thus cancelling out the GCF.
Example 2:
Write the rational expression in lowest terms:
Solution:
We can rewrite both the numerator and denominator by factoring to see what the GCF is and then simplify by using the fundamental property of rational numbers to cancel the GCF.
Example 3 :
Write the rational expression in lowest terms: 
Solution:
We can rewrite both the numerator and denominator by factoring to see what the GCF is and then simplify by using the fundamental property of rational numbers to cancel the GCF.
= 
Factor out –1 from the denominator.
= 
Cancel out the GCF .
= 
= – 1
Test Your Knowledge by opening up the Test Yourself Activity.
