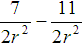Section 3: Adding and Subtracting Rational Expressions

It is important that you watch the video first.

Add and Subtract Rational Expressions with the Same Denominator

In algebra, adding or subtracting rational expressions is similar to that of add or subtracting fractions in arithmetic. The following steps will help you to add or subtract rational expressions.

Adding or Subtracting Rational Expressions

If the denominators are the same, add or subtract the numerators. Place the result over the common denominator.

If the denominators are different, first find the least common denominator. Write all rational expressions with this least common denominator, and then add or subtract the numerators. Place the result over the common denominator.
Simplify. Write all answers in lowest terms.

Example 1. Subtract

$Example 1a$

Solution.

Since the denominators are the same, all we need to do is subtract the numerators and keep the same denominator.

$Solution 1a$

This answer is not in lowest terms. It needs to be simplified.

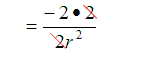
$solution 1b$

Apply the fundamental property of rational numbers.

$Solution 1c$

Example 2. Simplify

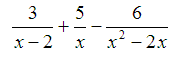
$Simplify ex2$

Solution.

Since the denominators are different, we first need to find the LCD. We follow the steps for find the LCD.

Step 1. Factor each denominator.

First denominator: x – 2 is already a single factor

Second denominator: x is already a single factor

LCD = x² – 2x = x(x – 2)
Step 2. We need to pick each different factor from each denominator, with each factor raised to the greatest power. In this example, the different factors are x and x – 2.

Therefore, the LCD = x · x – 2 = x(x – 2).

Now that we know the LCD, we need to rewrite the original two rational expressions with the LCD. In order to do so, we must multiply each expression (both numerator and denominator) by the factor needed to obtain the LCD in the denominator.

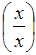
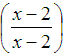
Multiply the first expression by $x over x$ to obtain the LCD, x(x – 2), in the denominator. Also, multiply the second expression by $x-2 divided by x -2$ to obtain the LCD, x(x – 2), in the denominator.

Finally, we multiplied the third expression by 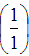$1 over 1$ to obtain the LCD, x(x – 2), in the denominator.

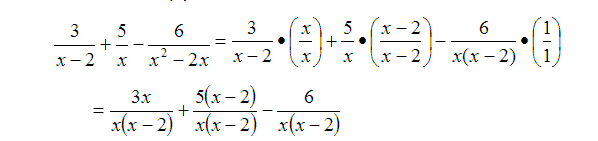
$third expression$

Now that we have the same denominator in all three expressions, we can add the numerators.

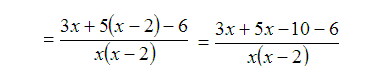
$same denominator$

Notice that the 5 was distributed in the numerator. Next, combine like terms.

$combine like terms$

Lastly, factor the GCF so that the fraction can be reduced.

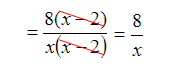
$reduce$

Test Your Knowledge by opening up the Test Yourself Activity.