Section 4: Simplifying Complex Fractions
It is important that you watch the video first.
Simplify Complex Fractions by Simplifying the Numerator and Denominator (Method 1)
A complex fraction is an expression having a fraction in the numerator, denominator, or both. Examples of complex fractions include:

There are two different methods for simplifying complex fractions. Method 1 is listed below.
Simplifying a Complex Fraction: Method 1
Step 1. Simplify the numerator and denominator separately.
Step 2. Divide by multiplying the numerator by the reciprocal of the denominator.
Step 3 Simplify the resulting fraction, if possible.
Example 1 : Simplify the complex fraction.
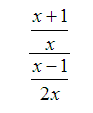
Solution:
Notice in this example that both the numerator and denominator are already simplified. Therefore, we go to step 2 which is to divide by multiplying the numerator by the reciprocal of the denominator.
Rewrite as a division problem by multiplying by the reciprocal of the denominator.
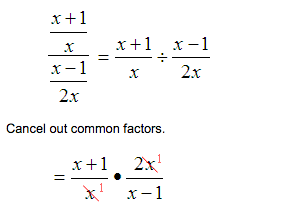
Cancel out common factors.

Multiply the remaining factors.

Simplifying a Complex Fraction: Method 2
Step 1. Multiply the numerator and denominator of the complex fraction by the least common denominator of the fractions in the numerator and the fractions in the denominator of the complex fraction.
Step 2. Simplify the resulting fraction, if possible.
Example 2. Use Method 2 to simplify the complex fraction.
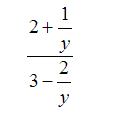
Solution.
Notice in this example that we need to simplify the numerator and denominator first. We need to find a common denominator for the numerator and for the denominator.
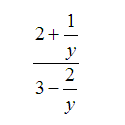
Notice that the LCD in both the numerator and denominator is y. Therefore, we rewrote both the numerator and denominator by multiplying by the factors needed to give us the common denominator.

Then we reduce the fractions within the numerator and denominator.

Test Your Knowledge by opening up the Test Yourself Activity.

