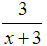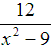Section 5: Solving Rational Equations
It is important that you watch the video first.
Determine the Domain of a Rational Equation
In algebra, the domain of a rational equation is the intersection (overlap) of the domains of the rational expressions in the equation. In other words, the intersection refers to those values that are contained in all of the domains
Example 1. Find the domain of the rational equation.
Solution
Since we have an equation that contains three rational expressions, we need to determine the domain of each expression and then find the intersection (overlap) of the three domains.
Recall that the domain of a rational expression is all real numbers except those that will make the denominator zero.
In the first expression,

the only value we can substitute for x that will turn the denominator into zero is 3. Therefore, the domain is all real numbers except 3 (written as {x│x ≠ 3}).
In the second expression
the only value we can substitute for x that will turn the denominator into zero is –3. Therefore, the domain is all real numbers except –3 (written as {x│x ≠ –3}).
For the last expression,
the values we can substitute for x that will turn the denominator into zero are 3 and –3. Therefore, the domain is all real numbers except 3 and –3 (written as {x│x ≠ ±3}).
Notice that the values contained in all three domains is all real numbers, but not 3 and –3
(recall
does not contain the number 3 in the domain and
does not contain the number –3 in the domain).
Therefore, the intersection of the three domains is all real numbers except 3 and –3 (written as {x│x ≠ ±3}).
Solve Rational Equations
To solve most equations with rational expressions we can multiply all terms in the equation by the least common denominator(LCD). This step will clear the equation of all denominators making the equation easier to solve. However, we must CHECK the solution to be sure that is in the domain.
Example 2.
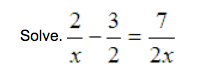
Solution.
Notice in this example that the least common denominator(LCD) is 2x. Therefore, we multiply the entire equation by the LCD.
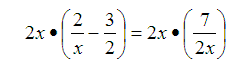
Distribute the LCD.

Multiply each term by LCD.
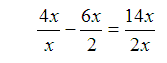
Simplify.
4 – 3x = 7
Solve for x.
4 – 3x – 4 = 7 – 4
– 3x = 3
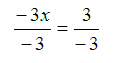
x = – 1

Substitute – 1 for x.
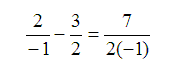
Simplify equation by finding the common denominator.
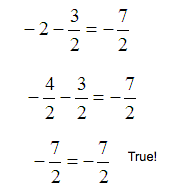
Therefore, the solution set is {– 1}.
Example 3. Solve.
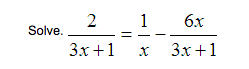
Solution. Notice in this example that the least common denominator (LCD) is x(3x + 1). Therefore, we multiply the entire equation by the LCD.
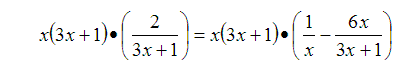
Multiply equation by the LCD
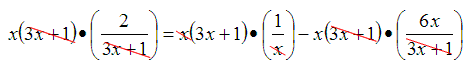
Distribute the LCD.
2x = (3x + 1) – x(6x)
Multiply to remove parenthesis.
2x = 3x + 1– 6x²
Since this equation is quadratic, we write it in standard form with 0 on the right side.
6x² – 3x +2x – 1 = 0
Combine like terms.
6x² – x – 1 = 0
Factor the left side of the equation.
(3x + 1)(2x – 1) = 0
Use the Zero-factor property.
3x + 1 = 0
or
2x – 1 = 0
| Solve for x in each equation. | ||
|---|---|---|
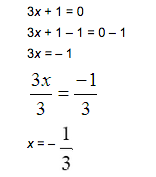 | or | 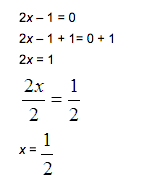 |
If we do the check for both answers, we will see that 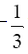 will not work (will give us a zero in the denominator in two fractions in the equation, meaning that
will not work (will give us a zero in the denominator in two fractions in the equation, meaning that 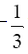 is not in the domain of the equation). Therefore, the solution set is
is not in the domain of the equation). Therefore, the solution set is 
Test Your Knowledge by opening up the Test Yourself Activity.